Muitos poderão pensar que a dívida pública e o défice público, se cingem a questões de opções políticas, mas na realidade uma das ciências que está bem presente em finanças públicas e economia, é a matemática. A iliteracia matemática de um certo povo, pode explicar em parte, o desequilíbrio que esse país tem nas suas finanças públicas, pois as mesmas nos estados democráticos, são muito afetadas por escolhas políticas. O modelo apresentado é um modelo simplificado, baseado em sistemas dinâmicos discretos, que explica como interagem a dívida, o défice e o crescimento económico de um Estado.
O défice público, simplificando, é a diferença entre as despesas e as receitas de um Estado. Quando um país tem mais receitas que despesas, tem superavit, ou excedente orçamental; quando esse país tem mais despesas que receitas, esse país tem défice. Quando há défice orçamental, o país necessita de contrair dívida para colmatar esse défice, que pagará com juros. Assim, um modelo simplificado do sistema poderá ser o seguinte
onde DVk, TJk e DFk são a Dívida, a Taxa de juro em percentagem e o Défice respetivamente no ano k. É fácil perceber que a Dívida no ano k+1, será a Dívida no ano k mais a componente dos juros, somando ainda o Défice do ano k.
Este modelo não inclui engenharias financeiras, nem contabilidade paralela, como sucedeu em Portugal com swaps, PPPs, ou dívidas contraídas pelas empresas públicas, se essas despesas não constarem nas contas oficiais do défice. Este modelo também obedece a outra simplificação. O Estado por norma contrai dívida através dos chamados títulos de dívida pública, emitidos com um certo prazo de maturidade, estando aquando da sua emissão já definidos a taxa de juro e o prazo. No modelo que se apresenta a Taxa de Juro aplica-se ao montante total da dívida no ano k, e não parcelado como realmente acontece com os títulos da dívida. Pode-se demonstrar que para períodos de tempo algo alargados, o erro deste modelo é bastante diminuto, se na Taxa de Juro se colocar o valor médio que o Estado tem pago de juros ao longo desse mesmo período de tempo.
Já o crescimento económico no ano k, ou seja o crescimento do valor do Produto Interno Bruto (PIB) do ano k para o ano k+1, ou seja CEk, obedece a outra equação semelhante
Já o crescimento económico no ano k, ou seja o crescimento do valor do Produto Interno Bruto (PIB) do ano k para o ano k+1, ou seja CEk, obedece a outra equação semelhante
Se dividirmos a primeira equação pelo PIB no ano k+1, multiplicando ainda implicitamente todos os termos da equação por 100, ficamos exatamente com uma outra equação, mas com a Dívida e o Défice, representados em percentagem do PIB.
onde DVp e DFp representam respetivamente a Dívida e o Défice em percentagem do PIB. Podemos ainda apresentar a equação acima de forma diferente, escrevendo
Se agora aplicarmos os conceitos da aproximação dos sistemas dinâmicos discretos aos sistemas dinâmicos contínuos obteremos uma equação diferencial linear de primeira ordem
A solução geral desta equação diferencial é
onde DVp(t) e DVp(0) representa a Dívida em percentagem do PIB no ano t e no ano 0 respetivamente, TJ a Taxa de juro da dívida, CE a percentagem de crescimento económico do PIB, e DFp o Défice público em percentagem do PIB.
E para o caso de Portugal (1980-2010)
Se considerarmos agora para o caso português, um período de cerca de 30 anos, de 1980 a 2010, com um défice público médio de aproximadamente 5%, uma taxa de juro média de 4% e um crescimento económico médio de 3%, ficamos com
A solução geral desta equação diferencial é
onde DVp(t) e DVp(0) representa a Dívida em percentagem do PIB no ano t e no ano 0 respetivamente, TJ a Taxa de juro da dívida, CE a percentagem de crescimento económico do PIB, e DFp o Défice público em percentagem do PIB.
E para o caso de Portugal (1980-2010)
Se considerarmos agora para o caso português, um período de cerca de 30 anos, de 1980 a 2010, com um défice público médio de aproximadamente 5%, uma taxa de juro média de 4% e um crescimento económico médio de 3%, ficamos com
cujo gráfico da expressão DVp é o seguinte:
 |
| Simulação segundo o modelo, t=0 corresponde a 1980; [1980,2010] Taxa de juro média da dívida de 4%, Crescimento económico de 3%, Défice Público médio de 3% |
Penso que a dívida pública apenas não atingiu os valores acima sugeridos pelo gráfico, cerca de 180% do PIB, porque o Estado foi alienando ativos que foram sendo abatidos à dívida, que muitas vezes não entravam nas contas do Défice, como algumas das sucessivas privatizações que se têm realizado desde 1980.
O decréscimo futuro da dívida exige obrigatoriamente excedente orçamental e/ou crescimento económico. A dívida que o modelo sugere, deveu-se essencialmente a variados anos de défices públicos sucessivos, com a agravante que à medida que em cada ano havia défice, contraía-se dívida, que por sua vez tinha de ser paga com juros. Este modelo demonstra que a dívida nestas condições de défices sucessivos tem um crescimento exponencial, que em situação de anos consecutivos de défices altos, leva à situação do crescimento exponencial acentuado da dívida, cujo controlo por parte do executivo, se torna crítico.
O que altera a dinâmica da Dívida neste sistema dinâmico, segundo o modelo, é a expressão TJ-CE, ou seja, a Taxa de Juro da dívida tem de ser inferior ao crescimento económico, para que a Dívida decresça.
O decréscimo futuro da dívida exige obrigatoriamente excedente orçamental e/ou crescimento económico. A dívida que o modelo sugere, deveu-se essencialmente a variados anos de défices públicos sucessivos, com a agravante que à medida que em cada ano havia défice, contraía-se dívida, que por sua vez tinha de ser paga com juros. Este modelo demonstra que a dívida nestas condições de défices sucessivos tem um crescimento exponencial, que em situação de anos consecutivos de défices altos, leva à situação do crescimento exponencial acentuado da dívida, cujo controlo por parte do executivo, se torna crítico.
O que altera a dinâmica da Dívida neste sistema dinâmico, segundo o modelo, é a expressão TJ-CE, ou seja, a Taxa de Juro da dívida tem de ser inferior ao crescimento económico, para que a Dívida decresça.
Resumidamente, poderá matematicamente comprovar-se aquilo que a generalidade dos cidadãos já tinha como implícito, que o défice de hoje, é a dívida de amanhã.

.gif)

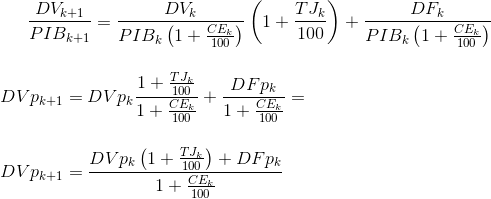.gif)
.gif)
.gif)
.gif)
.gif)
