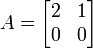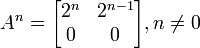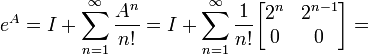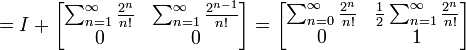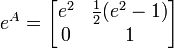Em matemática, a exponencial de uma matriz é uma função matricial definida no conjunto das matrizes quadradas e possui propriedades semelhantes função exponencial definida nos números reais (ou complexos). Mais abstratamente falando a exponencial matricial estabelece uma conexão entre a álgebra de Liedas matrizes e o seu correspondente grupo de Lie.
Seja  uma matriz real ou complexa
uma matriz real ou complexa 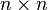 , define-se
, define-se  pela seguinte série de potências:
pela seguinte série de potências:
 uma matriz real ou complexa
uma matriz real ou complexa 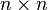 , define-se
, define-se  pela seguinte série de potências:
pela seguinte série de potências: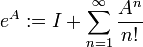 , onde
, onde  é a matriz identidade
é a matriz identidade
A convergência desta série é garantida pelo teste M de Weierstrass.
Propriedades
Sejam  e
e 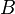 matrizes quadradas
matrizes quadradas 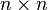 e
e  e
e  números reais ou complexos arbitrários. Denotamos por
números reais ou complexos arbitrários. Denotamos por  a matriz identidade
a matriz identidade 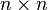 e por
e por 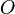 a matriz nula de mesmas dimensões.
a matriz nula de mesmas dimensões. 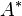 indica a matriz transposta conjugada de
indica a matriz transposta conjugada de  e
e 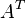 denota a matriz transposta de
denota a matriz transposta de  . São válidas as seguintes propriedades:
. São válidas as seguintes propriedades:
 e
e 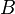 matrizes quadradas
matrizes quadradas 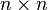 e
e  e
e  números reais ou complexos arbitrários. Denotamos por
números reais ou complexos arbitrários. Denotamos por  a matriz identidade
a matriz identidade 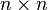 e por
e por 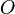 a matriz nula de mesmas dimensões.
a matriz nula de mesmas dimensões. 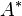 indica a matriz transposta conjugada de
indica a matriz transposta conjugada de  e
e 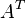 denota a matriz transposta de
denota a matriz transposta de  . São válidas as seguintes propriedades:
. São válidas as seguintes propriedades: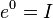
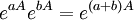
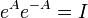
- Se
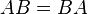 então
então 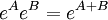
- Se
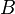 é uma matriz invertível então
é uma matriz invertível então 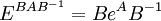
 , onde
, onde 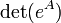 é o determinante de
é o determinante de 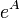 e
e 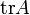 é o traço de
é o traço de 
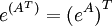 . Disto segue que se
. Disto segue que se  é uma matriz simétrica
é uma matriz simétrica 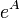 também o é. Se
também o é. Se  é uma matriz anti-simétrica é uma matriz ortogonal.
é uma matriz anti-simétrica é uma matriz ortogonal. . Disto segue que se
. Disto segue que se  é uma matriz hermitiana
é uma matriz hermitiana 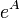 também o é. Se
também o é. Se  é uma matriz anti-hermitiana é uma matriz unitária.
é uma matriz anti-hermitiana é uma matriz unitária.
Exemplo no cálculo da exponencial de uma matriz
Imaginemos que queremos calcular eA sabendo que
Calculemos A2,A3...An
Sabemos então que
Este resultado pode ser conferido no Wolfram aqui.
Qualquer dúvida esclareça no fórum.