O critério da comparação, ou teste da comparação estabelece um método para aferir a convergência de séries positivas.
Sejam as séries:
Então se  , para todo o
, para todo o 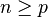 , e se a segunda série converge, então a primeira também converge (e tem soma inferior). Ou ainda, se a primeira diverge, então a segunda também diverge.
, e se a segunda série converge, então a primeira também converge (e tem soma inferior). Ou ainda, se a primeira diverge, então a segunda também diverge.
 , para todo o
, para todo o 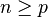 , e se a segunda série converge, então a primeira também converge (e tem soma inferior). Ou ainda, se a primeira diverge, então a segunda também diverge.
, e se a segunda série converge, então a primeira também converge (e tem soma inferior). Ou ainda, se a primeira diverge, então a segunda também diverge.Podemos também estabelecer que se 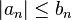 , então a primeira série converge contanto que a segunda também convirja.
, então a primeira série converge contanto que a segunda também convirja.
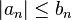 , então a primeira série converge contanto que a segunda também convirja.
, então a primeira série converge contanto que a segunda também convirja.Considermos as séries acima descritas e ainda o seguinte limite:
- se
![l \in \left]0,\infty\right[](https://upload.wikimedia.org/math/f/2/9/f29478c5c4365ea9b5d6046a7b756de5.png) as séries
as séries 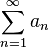 e
e 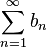 têm a mesma natureza.
têm a mesma natureza.
- se l = 0
-
- (a) se
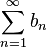 converge, então
converge, então 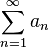 converge
converge - (b) se
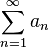 diverge, então
diverge, então 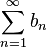 diverge
diverge
- (a) se
- se

-
- (a) se
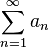 converge, então
converge, então 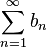 converge
converge - (b) se
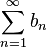 diverge, então
diverge, então 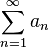 diverge
diverge
- (a) se
Qualquer dúvida ou esclarecimento não hesite em perguntar no fórum ou comentar aqui.

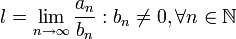
Relativamente ao 2º critério de comparação: se l=1, então nada podemos concluir acerca da convergencia da série em questão, certo? só podemos concluir que ambas têm a mesma natureza
ResponderEliminar