Em Matemática, o critério da razão ou critério d'Alembert é um teste para se saber se uma série é convergente ou não.
Seja 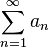 uma série de termos positivos.
uma série de termos positivos.
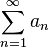 uma série de termos positivos.
uma série de termos positivos.Fazendo-se 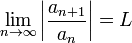
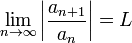
Se:
 a série é absolutamente convergente (portanto convergente)
a série é absolutamente convergente (portanto convergente)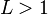 ou
ou  a série é divergente
a série é divergente o teste é inconclusivo
o teste é inconclusivo
Exemplo
Seja: 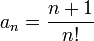
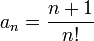
Clasificar 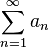
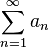
a) 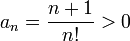
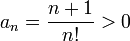
b) 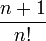 tende para zero quando n tende para infinito, pois n! cresce muito mais rapidamente que n.
tende para zero quando n tende para infinito, pois n! cresce muito mais rapidamente que n.
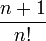 tende para zero quando n tende para infinito, pois n! cresce muito mais rapidamente que n.
tende para zero quando n tende para infinito, pois n! cresce muito mais rapidamente que n.c) Aplicando o critério D'Alembert:
e como L < 1, a série 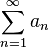 converge.
converge.
Qualquer dúvida que tenha ou sugestão deixe comentário.
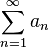 converge.
converge.Qualquer dúvida que tenha ou sugestão deixe comentário.

nem pegou do wiki!
ResponderEliminardeu para perceber
ResponderEliminarPeguei do wiki, mas fui eu quem contribuiu para o wiki
ResponderEliminarGostei desta
ResponderEliminar∑_(n=1)^∞▒(-1)^n *n/3^n
ResponderEliminar