O teste da raiz, critério da raiz ou teste de Cauchy é um teorema que permite estabelacer a convergência de uma série numérica. Muitas vezes, este teorema é também aplicado para estudar a convergência de uma série de funções e o respectivo raio de convergência.
Enunciado
Seja 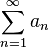 uma série numérica e a constante k definida pelo limite:
uma série numérica e a constante k definida pelo limite:
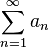 uma série numérica e a constante k definida pelo limite:
uma série numérica e a constante k definida pelo limite:Então:
- Se k < 1, a série converge absolutamente
- Se k > 1, a série diverge
- Se k = 1, nada se pode concluir
No caso de o limite não existir, este teste ainda é válido, substituindo a definição de k por:
Exemplo 1
Considere a série dada por:
Portanto a série converge.
Exemplo 2
Considere a série dada por:
![k=\lim_{n \to \infty} \sqrt[n]{|2^{n(-1)^n}|}=\lim_{n \to \infty} \sqrt[n]{|(2^{(-1)^n})^n|}
=\lim_{n \to \infty} \sqrt[n]{|2^{(-1)^n}|^n}=](https://upload.wikimedia.org/math/8/f/e/8fee7d5e0b0310dc2705c8e877fe4644.png)
 , em que:
, em que:
Então bn não tem limite, ou seja, 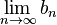 não existe.
não existe.
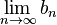 não existe.
não existe.Neste caso então, como o limite não existe, aplicaremos
Como 2 > 1, a série é divergente.

![k=\lim_{n \to \infty} \sqrt[n]{|a_n|}](https://upload.wikimedia.org/math/d/a/d/dad8ee7a419e29c18f1697105d05a84b.png)
![k=\limsup_{n \to \infty} \sqrt[n]{|a_n|}](https://upload.wikimedia.org/math/d/9/6/d96fb7f8cc89654d38d87a785a6a23d7.png)
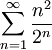
![k=\lim_{n \to \infty} \sqrt[n]{\frac{n^2}{2^n}}= \frac{1}{2}\lim_{n \to \infty} \sqrt[n]{n^2}=\frac{1}{2}<1](https://upload.wikimedia.org/math/c/d/d/cdd50affcf55b1a6399b0b522ca6474b.png)

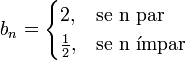
![k=\limsup_{n \to \infty} \sqrt[n]{|a_n|}=\limsup_{n \to \infty} (b_n) =2>1](https://upload.wikimedia.org/math/6/8/2/68230e3c01d8b5b3e74cd8c6e2f664a7.png)
muito bom, obrigado
ResponderEliminar