 |
| Triângulo rectângulo |
Pitágoras de Siracusa,
um dia disse aos netos,
o quadrado da hipotenusa
é igual à soma do quadrado dos catetos
Foi desta forma poética e sublime que enquanto criança obtive uma formulação matemática para um tratado geométrico tão ancestral como o Teorema de Pitágoras. Bem sei que Pitágoras era de Samos e não de Siracusa, e também há quem refira que parte deste teorema já era conhecido antes de Pitágoras pelos Babilónios, mas foi a Pitágoras que foi atribuído o cânone matemático supremo, metafísico e sacral. Diversa bibliografia refere Pitágoras como um iniciado e pertencente às sociedades secretas predecessoras da Maçonaria. Pitágoras fundou uma escola mística e filosófica em Crotona, que fazia parte das colónias gregas na península itálica; escola cujos princípios foram determinantes para a evolução geral da matemática e da filosofia ocidental sendo os principais temas a harmonia matemática, a doutrina dos números e o dualismo cósmico essencial.
Acredita-se que Pitágoras tenha sido casado com a física e matemática grega Theano, que foi sua aluna.
Os pitagóricos interessavam-se pelo estudo das propriedades dos números. Para eles, o número, sinónimo da harmonia, constituído da soma de pares e ímpares, pois os números pares e ímpares expressam as relações que se encontram em permanente processo de mutação; são considerados como a essência das coisas, criando noções opostas e sendo a base da teoria da harmonia das esferas.
Segundo os pitagóricos, o cosmos é regido por relações matemáticas. A observação dos astros sugeriu-lhes que uma ordem domina o Universo. Evidências disso estariam no dia e na noite, no alterar-se das estações e no movimento circular e perfeito das estrelas. Por isso o mundo poderia ser chamado de Cosmos, termo que contém as ideias de ordem, de correspondência e de beleza. Nessa cosmovisão também concluíram que a Terra é esférica, estrela entre as estrelas que se movem ao redor de um fogo central. Alguns pitagóricos chegaram até a falar da rotação da Terra sobre o eixo, mas a maior descoberta de Pitágoras ou dos seus discípulos, já que há obscuridades em torno do pitagorismo, devido ao carácter esotérico e secreto da escola, deu-se no domínio da geometria e se refere às relações entre os lados do triângulo rectângulo.
A descoberta foi enunciada no Teorema de Pitágoras.
A demonstração mais ancestral - Por comparação de áreas
 |
| Demonstração por comparação das áreas |
Não se sabe ao certo qual seria a demonstração utilizada por Pitágoras, entretanto, alguns autores concordam que ela teria sido feita através da comparação de áreas, conforme se segue:
- Desenha-se um quadrado de lado a + b;
- Traçam-se dois segmentos paralelos aos lados do quadrado;
- Divide-se cada um destes dois rectângulos em dois triângulos rectângulos, traçando as diagonais. Chama-se c o comprimento de cada diagonal;
- A área da região formada ao retirar os quatro triângulos rectângulos é igual a a2 + b2;
- Desenha-se agora o mesmo quadrado de lado a + b, mas colocamos os quatro triângulos rectângulos noutra posição.
- A área da região formada quando se retiram os quatro triângulos rectângulos é igual a c2.
Como a2 + b2 representa a área do quadrado maior subtraída da soma das áreas dos triângulos rectângulos, e c2 representa a mesma área, então a2 + b2 = c2. Ou seja, num triângulo rectângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. O segmento de medida c foi chamado de hipotenusa e os de medida b e a foram chamados de catetos.
Qualquer dúvida não hesite em deixar comentário!
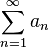 uma série numérica e a constante k definida pelo limite:
uma série numérica e a constante k definida pelo limite: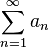 uma série numérica e a constante k definida pelo limite:
uma série numérica e a constante k definida pelo limite:![k=\lim_{n \to \infty} \sqrt[n]{|2^{n(-1)^n}|}=\lim_{n \to \infty} \sqrt[n]{|(2^{(-1)^n})^n|}
=\lim_{n \to \infty} \sqrt[n]{|2^{(-1)^n}|^n}=](https://upload.wikimedia.org/math/8/f/e/8fee7d5e0b0310dc2705c8e877fe4644.png)
 , em que:
, em que: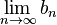 não existe.
não existe.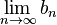 não existe.
não existe.
![k=\lim_{n \to \infty} \sqrt[n]{|a_n|}](https://upload.wikimedia.org/math/d/a/d/dad8ee7a419e29c18f1697105d05a84b.png)
![k=\limsup_{n \to \infty} \sqrt[n]{|a_n|}](https://upload.wikimedia.org/math/d/9/6/d96fb7f8cc89654d38d87a785a6a23d7.png)
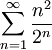
![k=\lim_{n \to \infty} \sqrt[n]{\frac{n^2}{2^n}}= \frac{1}{2}\lim_{n \to \infty} \sqrt[n]{n^2}=\frac{1}{2}<1](https://upload.wikimedia.org/math/c/d/d/cdd50affcf55b1a6399b0b522ca6474b.png)

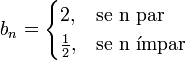
![k=\limsup_{n \to \infty} \sqrt[n]{|a_n|}=\limsup_{n \to \infty} (b_n) =2>1](https://upload.wikimedia.org/math/6/8/2/68230e3c01d8b5b3e74cd8c6e2f664a7.png)
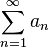 uma série de termos positivos.
uma série de termos positivos.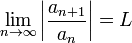
 a série é absolutamente convergente (portanto convergente)
a série é absolutamente convergente (portanto convergente)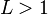 ou
ou  a série é divergente
a série é divergente o teste é inconclusivo
o teste é inconclusivo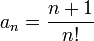
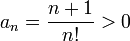
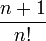 tende para zero quando
tende para zero quando 
