Colocaram-me, em tempos quando fui a uma entrevista de emprego o seguinte problema, imagine um recipiente com água, e no topo do recipiente encontra-se um cubo de gelo a flutuar, quando o gelo derreter como é que se alterará o nível da água? Manter-se-á? Aumentará ou diminuirá?
Custou-me a responder, e por certo que o entrevistador queria que eu tivesse uma noção sobre a alteração do estado da matéria e como tal, que me fosse intuitivo a alteração do volume dos objectos quando mudam de estado físico. O gelo embebido na água alterará o nível da água quando este derreter? Eu sabia que o gelo é menos denso que a água, e é por este mesmo facto que flutua, como tal haveria de ocupar mais espaço. Pensei à primeira vista que talvez o nível aumentasse devido a este facto.
Mas ao derreter lentamente, o cubo ao tornar-se mais leve, também haveria de ocupar menos espaço dentro de água, o que faria com que a água não subisse tanto, reflecti eu. Talvez este factor fosse compensador, e fizesse com que o nível da água se mantivesse. Iria dar a resposta sobre a qual havia reflectido: mantém-se. Mas de súbito, surgiu um dado empírico. Sempre ouvi dizer que o derretimento das calotas polares devido às alterações climáticas provocavam o aumento do nível médio da água do mar. Então a resposta que dei foi: aumenta.
Foi mais um dos casos em que deixei que os dados empíricos se sobrepusessem à intuição racional, e tal revelou-se num pensamento de cariz falacioso. Cheguei a casa e tentei aferir matemática e fisicamente através da álgebra qual o resultado correcto. Exponho aqui esse raciocínio:
Imaginemos um cubo de gelo de lado x que está emergido num recipiente com água. A base do recipiente é um quadrado de lado y. O gelo, suponhamos, tem apenas uma fracção de altura a emergida na água. A altura da água no estado inicial é hi . Depois do gelo derreter completamente, encontramo-nos no estado final, em que obviamente o recipiente é o mesmo, e em que teremos uma altura de água hf.
A figura seguinte tenta ser representativa daquilo que refiro:
É sabido que a densidade de um objecto é a sua massa sobre o seu volume
Pela lei de Arquimedes um corpo flutua quando o seu peso é igual ao peso de líquido deslocado onde flutua, ou seja neste caso
(2)
Em que MG é a massa do cubo de gelo, Mágua deslocada é a massa da água deslocada, g é a aceleração gravítica, ρg é a densidade do gelo, ρa é da densidade da água, x é o comprimento do lado do cubo de gelo e a é a porção de gelo que está submersa tal como está indicado na figura acima representada. Simplificando a fórmula acima descrita obtemos:
(3)
É sabido que depois do gelo derreter, a água daí resultante se mistura com a água inicial já existente no recipiente. Significa que a massa de gelo mais a massa de água inicial será igual à massa de água total no estado final, ou seja:
(4)
Nesta equação Ma é a massa de água inicial, MG é a massa do cubo de gelo e Mf é a massa total final depois do cubo de gelo derreter completamente. Desenvolvendo esta equação sabendo a equação em (1) e tendo em consideração a figura representada obtemos
Substituindo nesta equação, a variável a da equação (3), obtêm-se:
Conclui-se assim que a altura final é igual à inicial. Ou seja o derretimento do gelo quando está a flutuar, não provoca qualquer aumento no nível da água. É que a água é um dos raros elementos cujo estado sólido é menos denso que o seu estado líquido, por isso é que o gelo flutua. Simplificando, neste caso, o gelo ao derreter, faz com que a sua água equivalente vá ocupar exactamente o espaço que o gelo tinha embebido dentro da água do recipiente, verificando assim o princípio de Arquimedes. Este raciocínio poderá ser aplicado a todas as matérias que flutuem em que o objeto que flutua é do mesmo elemento que o líquido onde está embebido e que tenham as mesmas densidades antes e depois do derretimento, ou seja, da fusão do sólido. A flutuação só acontece quando o sólido é menos denso que o líquido.
O derretimento das calotas polares provoca o aumento do nível médio do mar, primeiramente porque uma grande parte do gelo em causa, como na Antártida ou na Gronelândia, está assente em rocha e não está a flutuar. Em segundo lugar, considerou-se no exercício, que a densidade da água depois do gelo derretido, e a densidade de água do recipiente antes do gelo derreter, eram a mesma, o que nem sempre é o caso. Caso consideremos densidades diferentes antes e depois do gelo derreter, ou seja ρ'a para a densidade inicial da água e ρa para a densidade final da água na equação (5) teremos:
o que resulta em:
onde ρ'a é a densidade inicial da água e ρa é a densidade final da água. Como muito do gelo que está a flutuar é composto por água mais doce em comparação à água do mar, tal resulta que 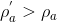 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
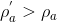 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:









