Colocaram-me, em tempos quando fui a uma entrevista de emprego o seguinte problema, imagine um recipiente com água, e no topo do recipiente encontra-se um cubo de gelo a flutuar, quando o gelo derreter como é que se alterará o nível da água? Manter-se-á? Aumentará ou diminuirá?
Custou-me a responder, e por certo que o entrevistador queria que eu tivesse uma noção sobre a alteração do estado da matéria e como tal, que me fosse intuitivo a alteração do volume dos objectos quando mudam de estado físico. O gelo embebido na água alterará o nível da água quando este derreter? Eu sabia que o gelo é menos denso que a água, e é por este mesmo facto que flutua, como tal haveria de ocupar mais espaço. Pensei à primeira vista que talvez o nível aumentasse devido a este facto.
Mas ao derreter lentamente, o cubo ao tornar-se mais leve, também haveria de ocupar menos espaço dentro de água, o que faria com que a água não subisse tanto, reflecti eu. Talvez este factor fosse compensador, e fizesse com que o nível da água se mantivesse. Iria dar a resposta sobre a qual havia reflectido: mantém-se. Mas de súbito, surgiu um dado empírico. Sempre ouvi dizer que o derretimento das calotas polares devido às alterações climáticas provocavam o aumento do nível médio da água do mar. Então a resposta que dei foi: aumenta.
Foi mais um dos casos em que deixei que os dados empíricos se sobrepusessem à intuição racional, e tal revelou-se num pensamento de cariz falacioso. Cheguei a casa e tentei aferir matemática e fisicamente através da álgebra qual o resultado correcto. Exponho aqui esse raciocínio:
Imaginemos um cubo de gelo de lado x que está emergido num recipiente com água. A base do recipiente é um quadrado de lado y. O gelo, suponhamos, tem apenas uma fracção de altura a emergida na água. A altura da água no estado inicial é hi . Depois do gelo derreter completamente, encontramo-nos no estado final, em que obviamente o recipiente é o mesmo, e em que teremos uma altura de água hf.
A figura seguinte tenta ser representativa daquilo que refiro:
É sabido que a densidade de um objecto é a sua massa sobre o seu volume
Pela lei de Arquimedes um corpo flutua quando o seu peso é igual ao peso de líquido deslocado onde flutua, ou seja neste caso
(2)
Em que MG é a massa do cubo de gelo, Mágua deslocada é a massa da água deslocada, g é a aceleração gravítica, ρg é a densidade do gelo, ρa é da densidade da água, x é o comprimento do lado do cubo de gelo e a é a porção de gelo que está submersa tal como está indicado na figura acima representada. Simplificando a fórmula acima descrita obtemos:
(3)
É sabido que depois do gelo derreter, a água daí resultante se mistura com a água inicial já existente no recipiente. Significa que a massa de gelo mais a massa de água inicial será igual à massa de água total no estado final, ou seja:
(4)
Nesta equação Ma é a massa de água inicial, MG é a massa do cubo de gelo e Mf é a massa total final depois do cubo de gelo derreter completamente. Desenvolvendo esta equação sabendo a equação em (1) e tendo em consideração a figura representada obtemos
Substituindo nesta equação, a variável a da equação (3), obtêm-se:
Conclui-se assim que a altura final é igual à inicial. Ou seja o derretimento do gelo quando está a flutuar, não provoca qualquer aumento no nível da água. É que a água é um dos raros elementos cujo estado sólido é menos denso que o seu estado líquido, por isso é que o gelo flutua. Simplificando, neste caso, o gelo ao derreter, faz com que a sua água equivalente vá ocupar exactamente o espaço que o gelo tinha embebido dentro da água do recipiente, verificando assim o princípio de Arquimedes. Este raciocínio poderá ser aplicado a todas as matérias que flutuem em que o objeto que flutua é do mesmo elemento que o líquido onde está embebido e que tenham as mesmas densidades antes e depois do derretimento, ou seja, da fusão do sólido. A flutuação só acontece quando o sólido é menos denso que o líquido.
O derretimento das calotas polares provoca o aumento do nível médio do mar, primeiramente porque uma grande parte do gelo em causa, como na Antártida ou na Gronelândia, está assente em rocha e não está a flutuar. Em segundo lugar, considerou-se no exercício, que a densidade da água depois do gelo derretido, e a densidade de água do recipiente antes do gelo derreter, eram a mesma, o que nem sempre é o caso. Caso consideremos densidades diferentes antes e depois do gelo derreter, ou seja ρ'a para a densidade inicial da água e ρa para a densidade final da água na equação (5) teremos:
o que resulta em:
onde ρ'a é a densidade inicial da água e ρa é a densidade final da água. Como muito do gelo que está a flutuar é composto por água mais doce em comparação à água do mar, tal resulta que 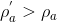 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
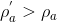 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:










Parece que não é só por isso:
ResponderEliminarhttp://www.physorg.com/news5619.html
!
---
"o gelo ao derreter, faz com que a sua água equivalente vá ocupar exactamente o espaço que o gelo tinha embebido dentro da água do recipiente," não toma em consideração que o gelo ocupa mais volume que a água 'equivalente'...
A explicação de que o nível não sobe tem de mostrar que o gelo que fica fora de água tem exactamente a quantidade de água necessária para preencher o excesso de volume que o gelo submerso tem. Só Arquimedes não dá porque há gelo que fica de fora e só o volume de água deslocado (pelo gelo submerso) é que provoca a subidas de nível.
Acho que o caro comentador está equivocado.
ResponderEliminarArquimedes é suficiente para prová-lo, e tal está descrito matematicamente acima. O gelo ao derreter vai ocupar exactamente o seu lugar equivalente que tinha embutido na água. Por isso é que o nível da água não sobe.
As calotas polares ao derreterem provocam o aumento do nível da água porque muito desse gelo não se encontra a boiar, logo este princípio não pode ser aplicado.
E não existe evaporação? Está esquecendo de mencionar.
EliminarJá percebi, já li o artigo isto refere-se a diferença entre água doce e água salgada e passo a citar:
ResponderEliminar"The common misconception that floating ice won’t increase sea level when it melts occurs because the difference in density between fresh water and salt water is not taken into consideration"
Agora para a mesma substância, para o mesmo elemento, não existe aumento do nível da água, e tal está correctamente atrás demonstrado...
O gelo formado nos polos não é da agua, e sim do ar. Por que há gelo numa montanha? A baixa temperatura que formou esse gelo do ar.
EliminarO fato de a água do mar ter densidade maior do que a do gelo não muda o fato de que o nível do mar não sobe. Matematicamente:
ResponderEliminarMgelo.grav = Mdesl.grav ->Mgelo = Mdesl
Mdesl + Mmar = Mfinal ->M = dens.V
dmar.Vdesl + dmar.Vmar = dfinal.Vfinal
(dmar/dfinal)(Vdesl + Vmar) = Vfinal
Ou seja, o nível só vai subir se a densidade do mar, depois do gelo derreter, for menor que a densidade do mar antes do gelo derreter. Mas isso só aconteceria se a quantidade de água no gelo fosse suficiente para mudar a densidade do mar, o que não vai acontecer.
Portanto, o nível do mar subiu mais de 100 metros desde a última era do gelo por causa do gelo em terra firme que derreteu.
Parabéns pelo site.
Não percebi a sua questão. O gelo que está no mar, tem derretido, a mesma densidade que a água do mar, logo o princípio é o mesmo, acho eu. O que sucede, é que grande parte dos blocos de gelo no planeta Terra estão assentes em rocha e não a flutuar no mar, daí o aumento do nível médio do mar, com o aquecimento global.
ResponderEliminarOu seja este sua frase: "portanto, o nível do mar subiu mais de 100 metros desde a última era do gelo por causa do gelo em terra firme que derreteu" está corretíssima.
Cumprimentos
Eu explico. As calotas polares são formadas por água doce, por isso possuem densidade menor que a água do mar, que possui sal. De acordo com a equação:
ResponderEliminar(dmar/dfinal)(Vdesl + Vmar) = Vfinal
se a quantidade de gelo derretido for suficiente para diminuir a densidade do mar, levando a dfinal < dmar, teremos dmar/dfinal > 1, então o volume final será igual ao volume inicial vezes um valor maior que um. Ou seja, o volume final será maior. Consequentemente, o nível do mar aumenta.
Abraço!
Muito obrigado pelo esclarecimento
ResponderEliminarCumprimentos
Parabens! Muito bom.
ResponderEliminarOlá, boa dedução, mas na equação (5), quando se desconta o volume do gelo, penso que não deveria ser considerado a dimensão do cubo de gelo (x), pois ao mudar de fase, os lados desse cubo seriam menores, assim como a altura "a", ou seja, o espaço ocupado inicialmente pelo cubo seria menor devido à contração ocasionada pela mudança de fase. Sendo assim, hf<hi. Concorda? Um resultado, em princípio, seria considerar uma contração em volume como uma relação entre as densidades do gelo e da água (0,92 e 1,0). Assim, na equação (5), teria que ser considerado uma retração de ~1/0,92 ou 8,7%.
ResponderEliminar